1) ovule or pollen-bearing structure of conifers. 2) a bright-colored traffic control device used to isolate areas on work sites from pedestrians or vehicles.
A cone is a three-dimensional geometric shape that tapers smoothly from a flat base (frequently, though not necessarily, circular) to a point called the apex or vertex.
A cone is formed by a set of line segments, half-lines, or lines connecting a common point, the apex, to all of the points on a base that is in a plane that does not contain the apex. Depending on the author, the base may be restricted to be a circle, any one-dimensional quadratic form in the plane, any closed one-dimensional figure, or any of the above plus all the enclosed points. If the enclosed points are included in the base, the cone is a solid object; otherwise it is a two-dimensional object in three-dimensional space. In the case of a solid object, the boundary formed by these lines or partial lines is called the lateral surface; if the lateral surface is unbounded, it is a conical surface.
In the case of line segments, the cone does not extend beyond the base, while in the case of half-lines, it extends infinitely far. In the case of lines, the cone extends infinitely far in both directions from the apex, in which case it is sometimes called a double cone. Either half of a double cone on one side of the apex is called a nappe.
The axis of a cone is the straight line (if any), passing through the apex, about which the base (and the whole cone) has a circular symmetry.
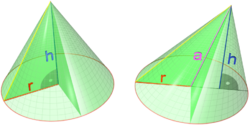
In common usage in elementary geometry, cones are assumed to be right circular, where circular means that the base is a circle and right means that the axis passes through the centre of the base at right angles to its plane. If the cone is right circular the intersection of a plane with the lateral surface is a conic section. In general, however, the base may be any shape and the apex may lie anywhere (though it is usually assumed that the base is bounded and therefore has finite area, and that the apex lies outside the plane of the base). Contrasted with right cones are oblique cones, in which the axis passes through the centre of the base non-perpendicularly.
A cone with a polygonal base is called a pyramid.
Depending on the context, "cone" may also mean specifically a convex cone or a projective cone.
Cones can also be generalized to higher dimensions.